Chapter contents:
Geological time
– 1. Relative age dating
– 2. Absolute age dating ←
– 3. Geological time scale
– 4. Geological maps
Absolute age dating deals with assigning actual dates (in years before the present) to rocks or geological events. Contrast this with relative age dating, which instead is concerned with determining the orders of events in Earth's past. The science of absolute age dating is known as geochronology and the fundamental method of geochronology is called radiometric dating.
Scholars and naturalists, understandably, have long been interested in knowing the absolute age of the Earth, as well as other important geological events. In 1650, Archbishop James Ussher famously used the genealogy of the Old Testament of the Bible (e.g., Genesis, Chapter 5)--and the human lifespans recorded in it--to estimate the age of the Earth; he concluded that the Earth was young in age, having formed in 4004 B.C., or about 6,000 years ago.

Archbishop James Ussher (1581-1656) (public domain; WikiMedia Commons).
In the 1800's, practitioners of the young science of geology applied the uniformitarian views of Hutton and Lyell (see the introduction to this chapter) to try to determine the age of the Earth. For example, some geologists observed how long it took for a given amount of sediment (say, a centimeter of sand) to accumulate in a modern habitat, then applied this rate to the total known thickness of sedimentary rocks. When they did this, they estimated that the Earth is many millions of years old.
We now know that this estimate is far, far too young*. But, unlike Ussher's calculation, this estimate was on the order of millions of years, rather than 6,000. Geologists were beginning to accept the views of Hutton that the Earth is unimaginably ancient. [*In part, this estimate is so low because these early geologists did not recognize that unconformities--which represent missing units of time, often caused by erosion--are rampant in the rock record, as well as the fact that some metamorphic rocks were once sedimentary, and thus left out of their calculations.]
What key discovery, then, allowed geologists to begin assigning absolute age dates to rocks and ultimately discover the age of the Earth? The answer is radioactivity.
Radiometric dating
Hypotheses of absolute ages of rocks (as well as the events that they represent) are determined from rates of radioactive decay of some isotopes of elements that occur naturally in rocks.
Elements and isotopes
In chemistry, an element is a particular kind of atom that is defined by the number of protons that it has in its nucleus. The number of protons equals the element's atomic number. Have a look at the periodic table of the elements below. Carbon's (C) atomic number is 6 because it has six protons in its nucleus; gold's (Au) atomic number is 79 because it has 79 atoms in its nucleus.

Periodic table of the elements. Image by Sandbh - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=55162370.
Even though individual elements always have the same number of protons, the number of neutrons in their nuclei sometimes varies. These variations are called isotopes. Isotopes of individual elements are defined by their mass number, which is simply the number of protons + the number of neutrons.
Consider, for example, the three different isotopes of Carbon:
- Carbon-12: 6 protons, 6 neutrons
- Carbon-13: 6 protons, 7 neutrons
- Carbon-14: 6 protons, 8 neutrons
Most isotopes are stable, meaning that they do not change. Some isotopes are unstable, however, and undergo radioactive decay.
Radioactive decay
Radioactive decay involves unstable isotopes shedding energy in the form of radiation, causing their numbers of protons and neutrons to change, in turn resulting in one element changing into another.
As a matter of convention, we call the atomic nucleus that undergoes radioactive decay the parent and the resulting product the daughter product (or, decay product).
The rate at which a particular parent isotope decays into its daughter product is constant. This rate is determined in a laboratory setting and is typically represented by its half-life. A half-life is the amount of time needed for half of the parent atoms in a sample to be changed into daughter products. This is illustrated in the chart below.
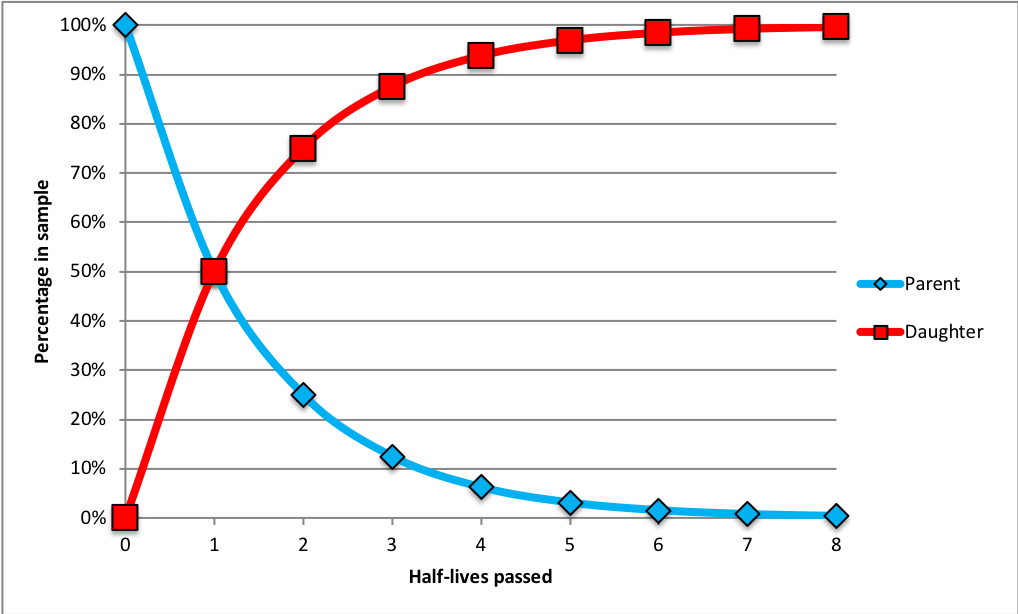
Relationship between the amount of radioactive parent atoms in a sample relative to the number of daughter atoms over the passage of time, measured in half-lives. Image by Jonathan R. Hendricks.  This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
At the start time (zero half-lives passed), the sample consists of 100% parent atoms (blue diamonds); there are no daughter products (red squares) because no time has passed. After the passage of one half-life, 50% of the parent atoms have become daughter products. After two half-lives, 75% of the original parent atoms have been transformed into daughter products (thus, only 25% of the original parent atoms remain). After three half-lives, only 12.5% of the original parent atoms remain. As more half-lives pass, the number of parent atoms remaining approaches zero.
Based on this principle, geologists can count the number of parent atoms relative to daughter products in a sample to determine how many half-lives have passed since a mineral grain first formed. Consider the example shown below.
An example of how the initial number of radioactive parent atoms (blue diamonds) in two mineral grains (gray hexagons) changes over time (measured in half-lives) relative to the number of daughter products (red squares). Image by Jonathan R. Hendricks.  This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
The left-most box in the figure above represents an initial state, with parent atoms distributed throughout molten rock (magma). As the magma cools, grains of different minerals begin to crystalize. Some of these minerals (represented above as gray hexagons) incorporate the radioactive parent atoms (blue diamonds) into their crystalline structures; this marks the initiation of the "half-life clock" (i.e., the start time, or time zero). After one half-life has passed, half (50%, or four) of the parent atoms in each mineral grain have been transformed into their daughter products (red squares). After two half-lives have passed, 75% (six) of the original parent atoms in each grain have been transformed into daughter products. How many parent atoms would remain if three half-lives passed?
Calculating radiometric dates
By counting the numbers of parent atoms remaining in a sample relative to the number originally present, it is possible to determine the number of half-lives that have passed since the initial formation of a mineral grain (that is, when it became a "closed system" that prevented parent and daughter atoms from escaping). You might be wondering how it is possible to know the number of parent atoms that were originally in a sample. This number is attained by simply adding the number of parent and daughter atoms currently in the sample (because each daughter atom was once a parent atom).
The next step in radiometric dating involves converting the number of half-lives that have passed into an absolute (i.e., actual) age. This is done by multiplying the number of half-lives that have passed by the half-life decay constant of the parent atom (again, this value is determined in a laboratory).
To summarize, the key piece of information that needs to be determined from a mineral specimen in order to determine its absolute age is its age in number of half lives.
This can be mathematically determined by solving for y in this equation:
Np / N0 = (1 - λ)y
where Np = the number of parent atoms currently in the sample, N0 = number of parent atoms present in the sample when the system became closed (so, N0 = Np + Nd, where Nd = the number of daughter atoms currently in the sample), λ = the decay constant, which for half-life is 0.5, and y = the number of half-lives that have passed.
Let's work through a hypothetical example problem. Suppose you analyzed a mineral sample and found that it contained 33,278 parent atoms and 14,382 daughter atoms. Further, suppose that the half-life of the parent atom is 2.7 million years. How old is the mineral sample?
First, we know that: Np = 33,278; N0 = Np + Nd = 33,278 + 14,382 = 47,660; and that λ = 0.5. So,
Np / N0 = (1 - λ)y
33,278 / 47,660 = (1 - 0.5)y
0.698 = 0.5y
log 0.698 = y * log 0.5
log 0.698 / log 0.5 = y
-0.156 / -0.301 = y
y = 0.518
So, we conclude that 0.518 half-lives have passed since the formation of this mineral sample. To determine the absolute age of this mineral sample, we simply multiply y (=0.518) times the half life of the parent atom (=2.7 million years).
Thus, the absolute age of sample = y * half-life = 0.518 * 2.7 million years = 1.40 million years.
As noted above, a radiometric date tells us when a system became closed, for example when a mineral containing radioactive parent elements first crystalized. An individual mineral grain may have a long history after it first forms. For example, it may erode out of an igneous rock and then be transported long distances and over long periods of time before it is finally deposited, becoming one grain among billions in a layer of sedimentary rock (e.g., sandstone). If a radiometric date were to be attained from this mineral grain, it would tell us when the mineral first formed, but not when the sedimentary rock formed (it would, however, tell us the maximum possible age of the sedimentary rock layer).
Further, heating mineral grains to great temperatures can cause them to leak parent and daughter material, resetting their radiometric clocks. This can be a concern when calculating radiometric dates from samples of metamorphic rocks, which are sedimentary or igneous rocks that have been altered by great amounts of heat and/or pressure. The melting involved with metamorphic change can reset the radiometric clock. For example, suppose an igneous rock formed 2.0 billion years ago. If it were subjected to metamorphism 1.2 billion years ago, radiometric dating would tell us that a sample from the rock is 1.2 billion years old, not 2.0 billion years old.
Variation in half-lives among different isotopes
As noted above, the rate at which a given radioactive isotope decays into its daughter product is constant. This rate, however, varies considerably among different radioactive isotopes. Further, many radioactive isotopes undergo a series of transformations--some of which have half-lives that persist for only very short amounts of time--before they are converted into their final daughter products.
Below are some of the decay series that are commonly used in radiometric dating of geological samples. Note the great variations in their half-lives.
| Parent isotope | Final decay product | Half-life |
|---|---|---|
| Uranium-238 | Lead-206 | 4.47 billion years |
| Uranium-235 | Lead-207 | 710 million years |
| Potassium-40 | Argon-40 | 1.25 billion years |
| Rubidium-87 | Strontium-87 | 50 billion years |
| Carbon-14 | Nitrogen-14 | 5,730 years |
Note that the half-life for the rubidium-87 to strontium-87 series is 50 billion years! Since the entire universe is 13.8 billion years old, we know that not enough time has passed for even half (i.e., one half-life) of the universe's supply of rubidium-87 to decay into strontium-87.
At the other end of the spectrum, note the very short half-life of carbon-14: 5,730 years. The is the isotope that is used in "carbon dating." Carbon-14 forms in Earth's upper atmosphere. Both it and carbon-12 (which is stable, meaning that it does not undergo radioactive decay) are incorporated into the tissues of plants as they grow. After a plant dies, the carbon-12 in its tissues remains stable, but the carbon-14 decays into nitrogen-14. The ratio of carbon-14 relative to carbon-12 in a sample, therefore, may be used to determine the age of organic matter derived from plant tissues. Because of its short half-life, carbon-14 can only be used to date materials that are up to about 70,000 years old (beyond this point, the amount of carbon-14 remaining becomes so small that it is difficult to measure). Because of its precision, it is nevertheless very useful for dating organic matter from the near recent geological past, especially archeological materials from the Holocene epoch.
Age of the Earth
At the beginning of this chapter, you learned that the Earth is 4.54 billion years old. As it turns out, the oldest dated mineral--a grain of zircon from the Jack Hills of Western Australia--is 4.4 billion years old and the oldest known rock unit--the Acasta Gneiss from the Northwest Territories of Canada--is 4.0 billion years old.

A single grain of zircon, imaged using a scanning electron microscope. Image by Gunnar Ries, Creative Commons BY-SA 2.5.

A sample of 4.0 billion year old Acasta Gneiss from the Northwest Territories of Canada. Image by Mike Beauregard, Wikimedia Commons, Creative Commons Attribution 2.0 Generic license.
If the oldest mineral grain is 4.4 Ga and the oldest rock 4.0 Ga, how then do we know that the Earth is 4.54 Ga? The answer is radiometric dating of meteorite specimens, which we presume to have formed around the same time as the Earth, Sun, and other planetary bodies in our solar system. One such dated meteorite comes from Meteor Crater in Arizona.

The Holsinger Meteorite, which is a piece of the meteor that crashed in ancient Arizona, forming Meteor Crater. Samples from this meteor were used by Clair Patterson to determine the age of the Earth. Image by Marcin Wichary - originally posted to Flickr as The biggest discovered fragment, CC BY 2.0, Link
Review
Question
True or False: It is generally not possible to use carbon dating to date samples older than 70,000 years.
Answer
True.
Question
After three half-lives, what percentage of the original radioactive parent isotope will remain in a sample?
Answer
12.5% (1st half-life: 50%; 2nd half-life: 25%; 3rd half-life 12.5%).
Question
What key discovery allowed scientists to begin measuring the absolute ages of rock samples?
Answer
Radioactivity.
Question
True or False: Different isotopes of the same element vary in their numbers of protons.
Answer
False. They vary in their numbers of neutrons.
Question
True or False: The age of the Earth was determined by dating a rock sample found at the bottom of the Grand Canyon.
Answer
False. It was determined by dating meteorite samples.
Question
If you know the number of radioactive parent atoms remaining in a sample, as well as the number originally present, what additional key piece of information is needed to calculate the age of the sample?
Answer
Half-life decay constant.
Question
True or False: Radioactive isotopes of different elements decay at the same rate.
Answer
False. They decay at different rates.
Question
Adding the number of protons and the number of neutrons in an atom gives you what value?
Answer
Atomic mass number.


